本文共 799 字，大约阅读时间需要 2 分钟。

先上代码:

public class FileInAndOut {
   	public static void main(String[] args) {
   		//定义指定磁盘的文件的File对象		File file = new File("E:/大三下学期/Android/作业要求/java知识巩固/work5.txt");				if(! file.exists()){
   			System.out.println("对不起，不包含指定路径的文件");		}else{
   			//根据指定路径的File对象创建FileReader对象			try {
   				FileReader fr = new FileReader(file);								char[] data = new char[51];			//定义char数组								int length = 0;								while((length = fr.read(data))>0){
   			//循环读取文件中的数据					String str = new String(data,0,length);			//根据读取文件的内容创建String 对象					System.out.println(str);				//输出读取内容				}				fr.close();								//关闭流			} catch (Exception e) {
   				// TODO Auto-generated catch block				e.printStackTrace();			}		}	}}

控制台输出结果如下:

原因是

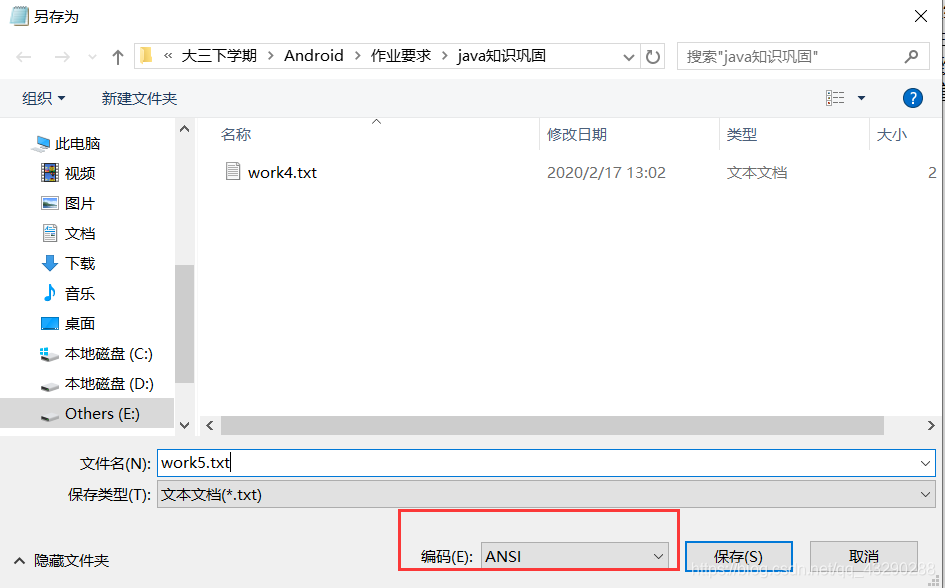
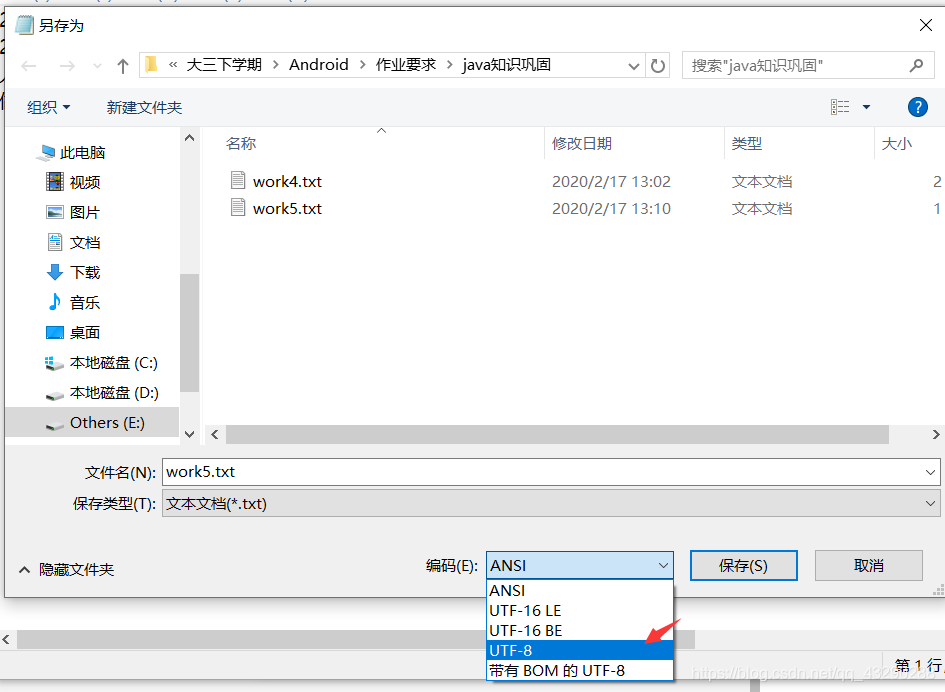
运行之后的结果为

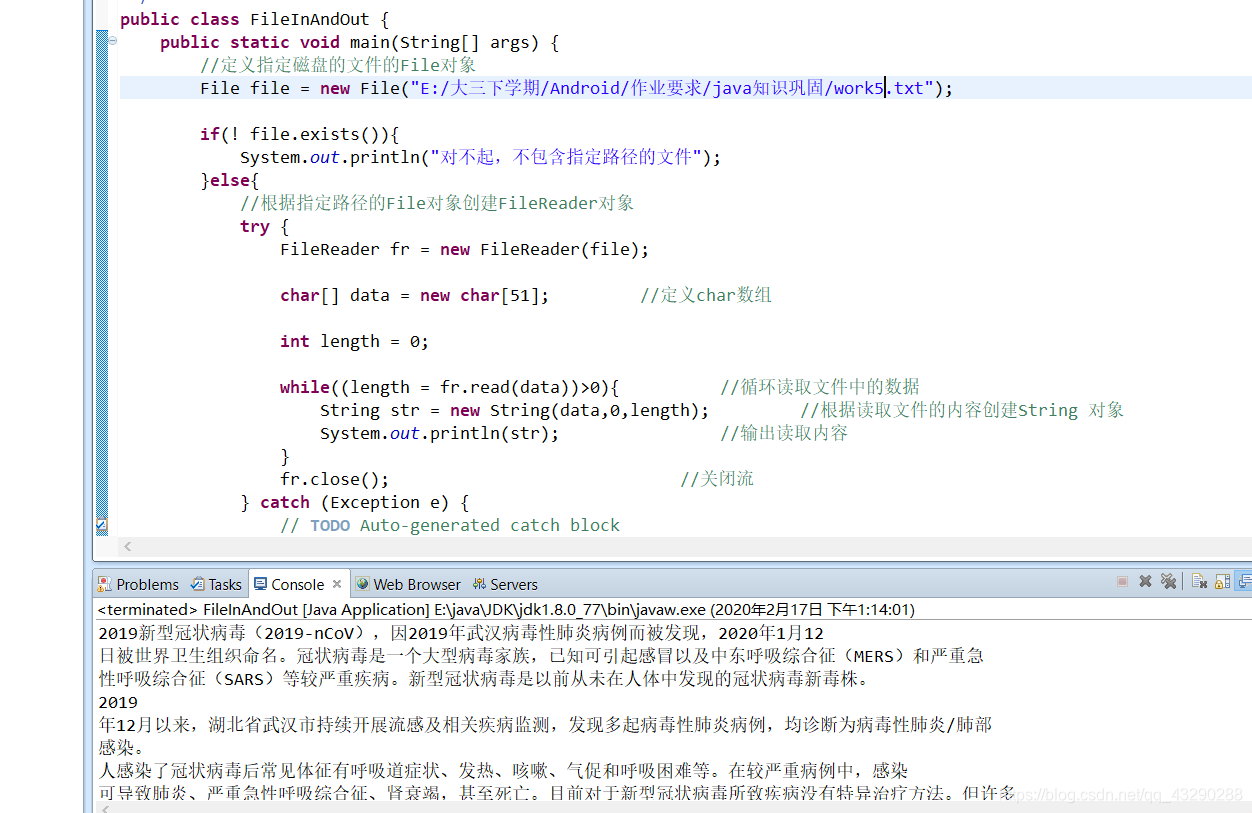
转载地址：http://cooq.baihongyu.com/